数据结构学习笔记---线性排序

排序

Word count: 1.7kReading time: 6 min

 2020/03/30   Share

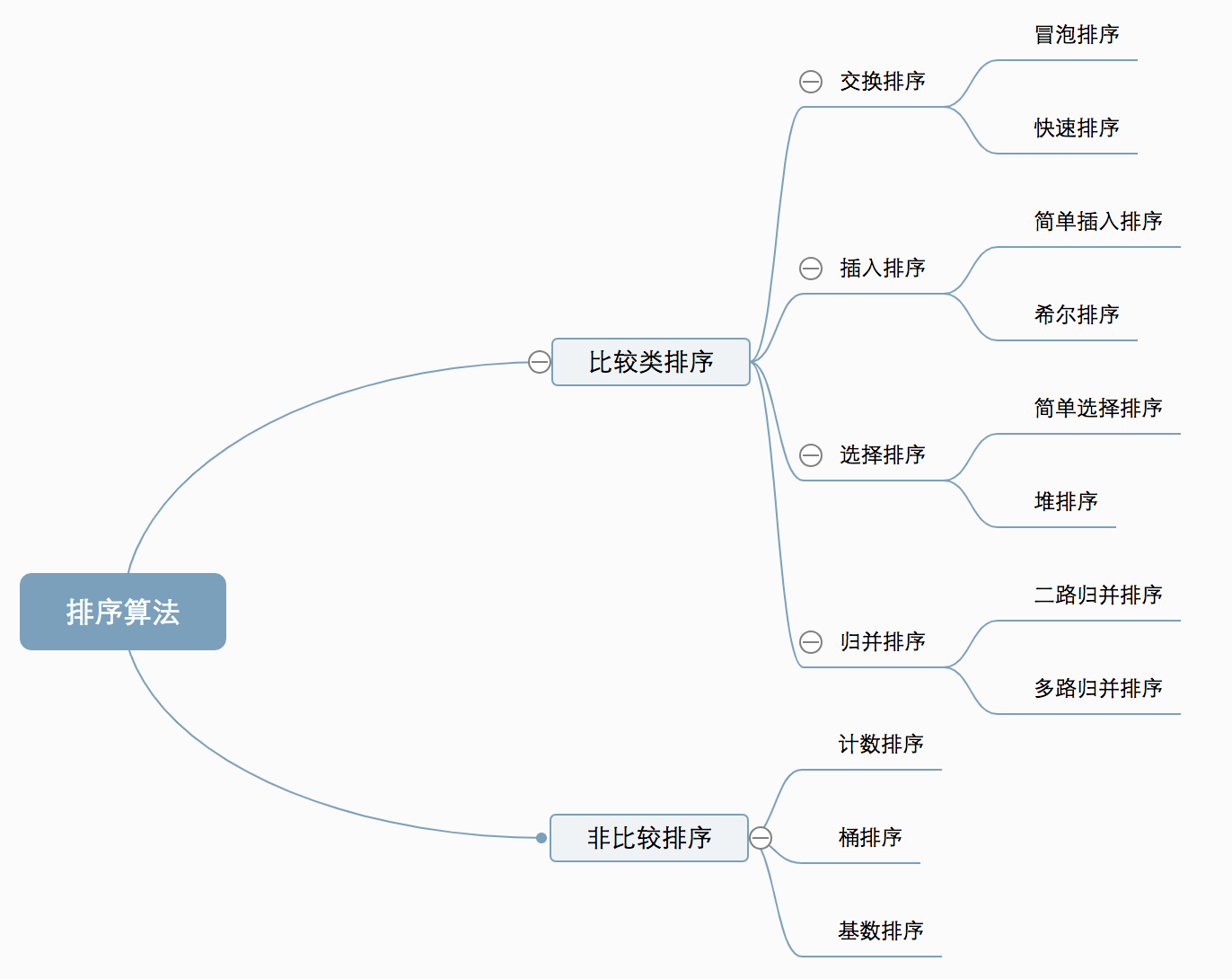
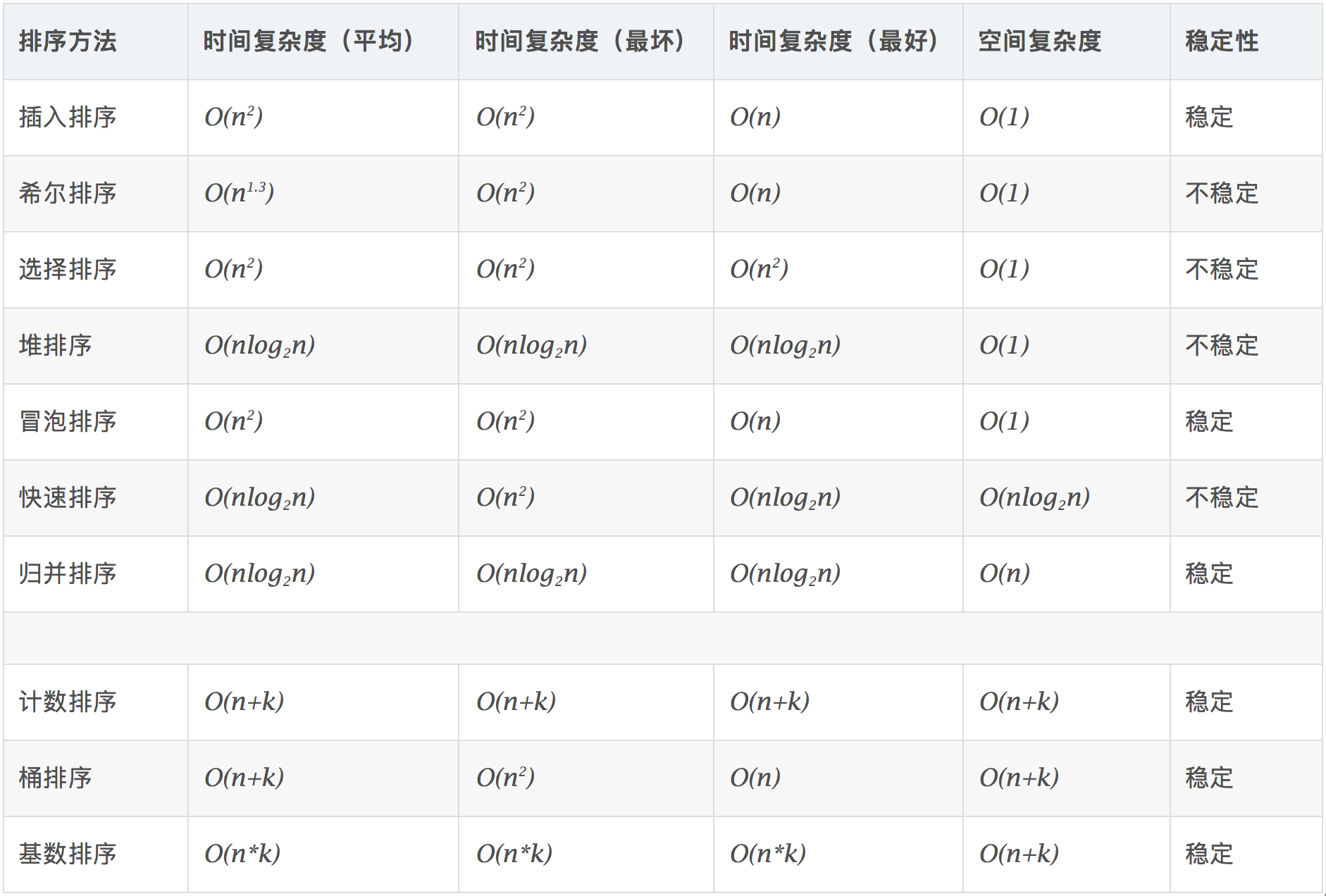
学习自极客时间的《数据结构与算法之美》作者：王争

1. 桶排序（Bucket sort）

桶排序，顾名思义，会用到“桶”，核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

def bucketSort(nums):
  # 选择一个最大的数
  max_num = max(nums)
  # 创建一个元素全是0的列表, 当做桶
  bucket = [0]*(max_num+1)
  # 把所有元素放入桶中, 即把对应元素个数加一
  for i in nums:
    bucket[i] += 1
  # 存储排序好的元素
  sort_nums = []
  # 取出桶中的元素
  for j in range(len(bucket)):
    if bucket[j] != 0:
      for y in range(bucket[j]):
        sort_nums.append(j)
  return sort_nums

桶排序的时间复杂度

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

桶排序的缺点

桶排序对要排序数据的要求是非常苛刻的。

首先，要排序的数据需要很容易就能划分成 m 个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后，桶与桶之间的数据不需要再进行排序。
其次，数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后，有些桶里的数据非常多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了。在极端情况下，如果数据都被划分到一个桶里，那就退化为 O(nlogn) 的排序算法了。

桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。

2. 计数排序（Counting sort）

计数排序其实是桶排序的一种特殊情况。当要排序的 n 个数据，所处的范围并不大的时候，比如最大值是 k，我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。

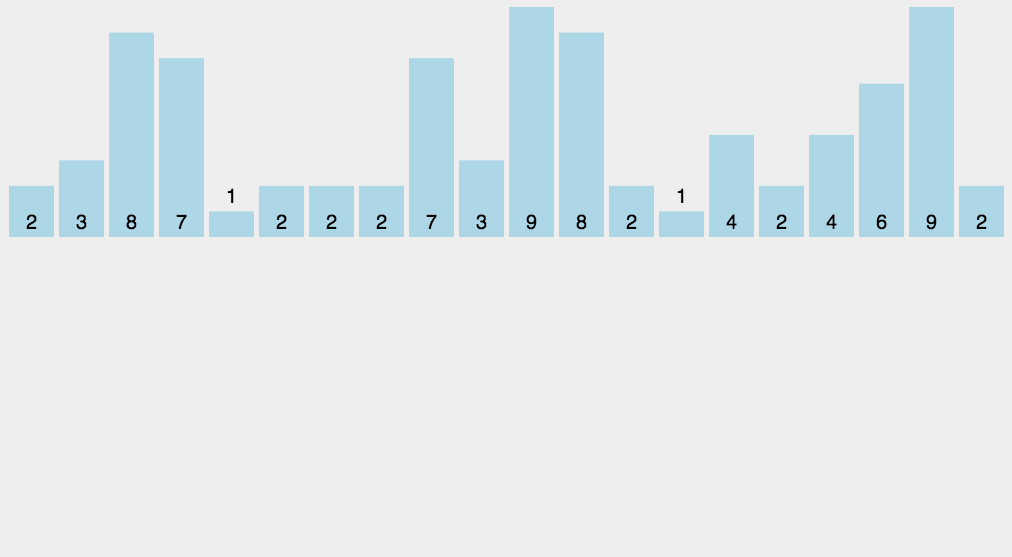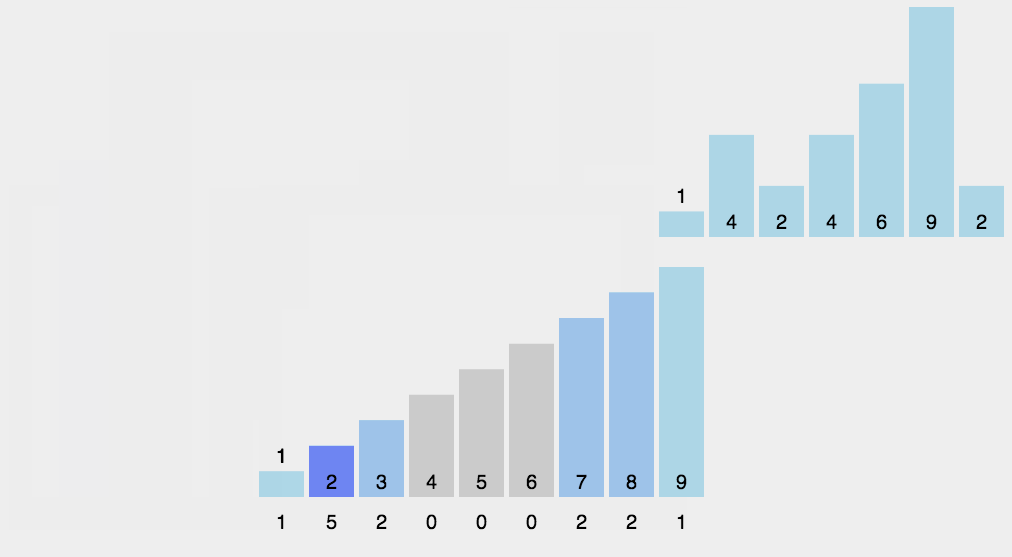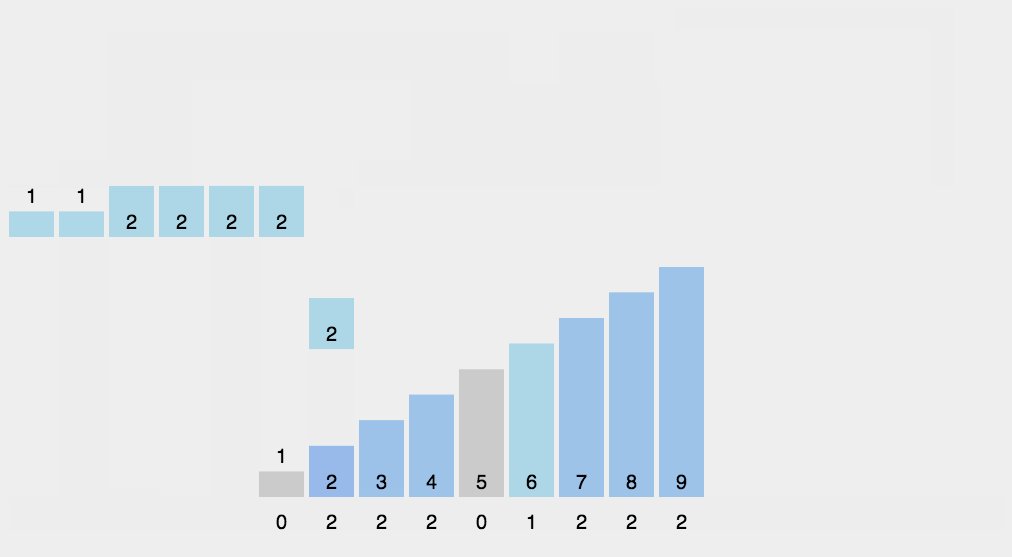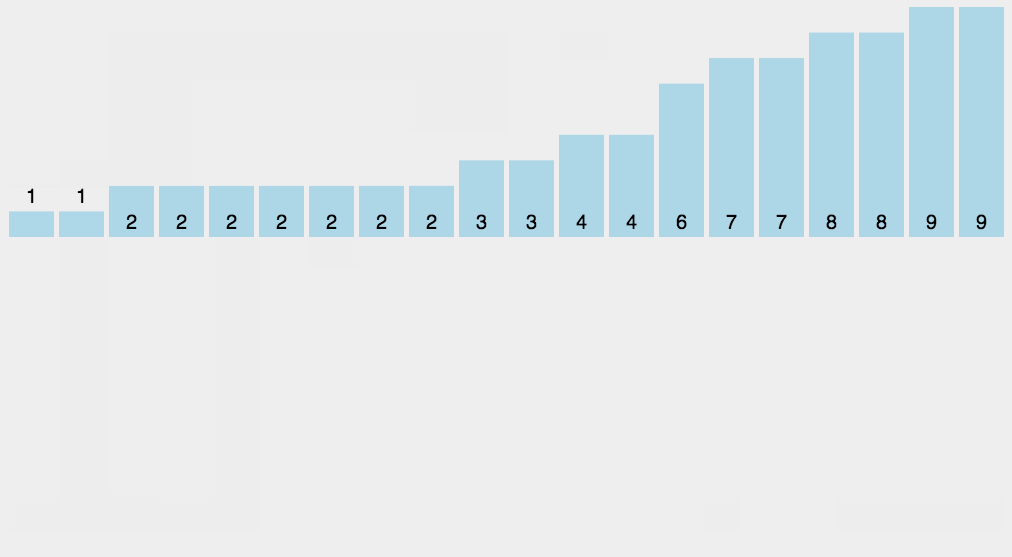
def countingSort(arr):
    max_value = max(arr)
    bucket_len = max_value + 1
    # 每一个数都申请一个桶
    bucket = [0] * bucket_len
    sorted_index = 0
    arr_len = len(arr)
    for i in range(arr_len):
        # 索引号为该数字时,计数加一
        bucket[arr[i]] += 1
    for j in range(bucket_len):
        while bucket[j] > 0:
            arr[sorted_index] = j
            sorted_index += 1
            bucket[j] -= 1
    return arr

计数排序的优化

如何快速计算出，每个数在有序数组中对应的存储位置呢？这个处理方法非常巧妙，很不容易想到。
假设只有 8 个数字，分数在 0 到 5 分之间。这 8 个数字的值我们放在一个数组 A[8]中，它们分别是：2，5，3，0，2，3，0，3。

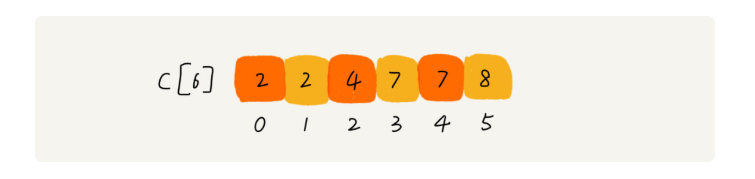
我们使用大小为 6 的数组 C[6]表示桶，其中下标对应分数。不过，C[6]内存储的并不是考生，而是对应的考生个数。像我刚刚举的那个例子，我们只需要遍历一遍考生分数，就可以得到 C[6]的值。
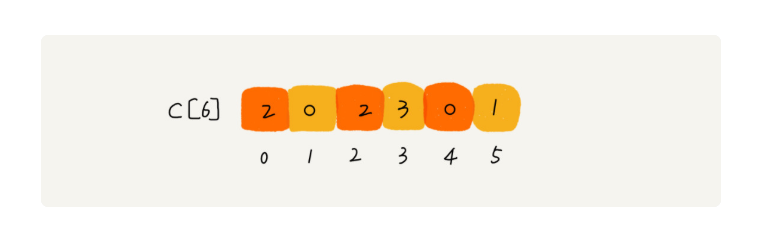
分数为 3 分的考生有 3 个，小于 3 分的考生有 4 个，所以，成绩为 3 分的考生在排序之后的有序数组 R[8]中，会保存下标 4，5，6 的位置。
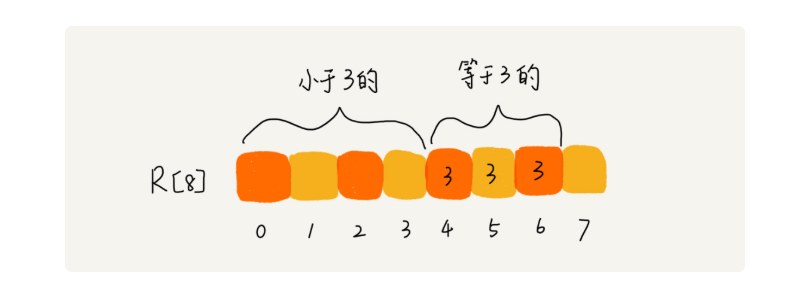
我们对 C[6]数组顺序求和，C[6]存储的数据就变成了下面这样子。C[k]里存储小于等于分数 k 的考生个数。
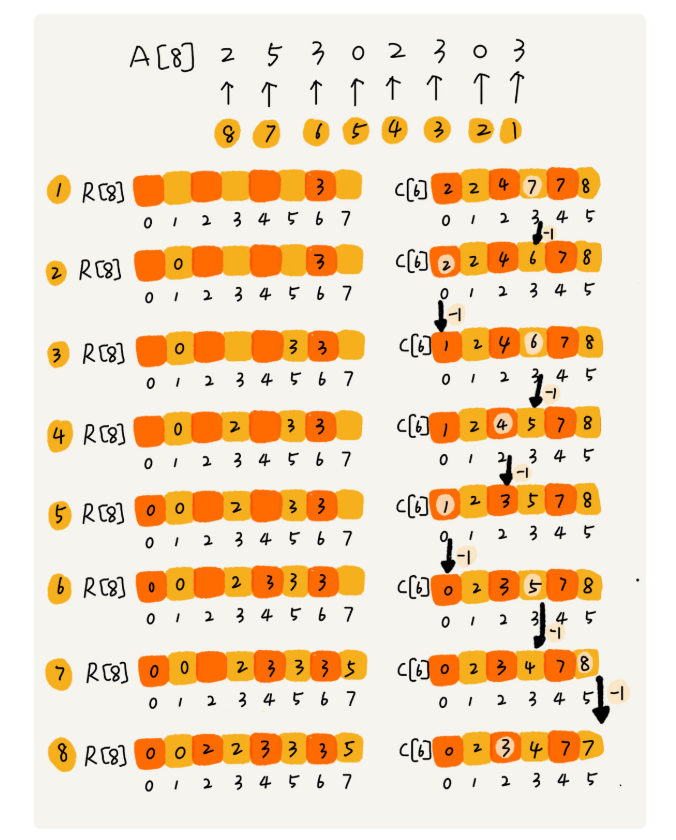
从后到前依次扫描数组 A。比如，当扫描到 3 时，我们可以从数组 C 中取出下标为 3 的值 7，也就是说，到目前为止，包括自己在内，分数小于等于 3 的考生有 7 个，也就是说 3 是数组 R 中的第 7 个元素（也就是数组 R 中下标为 6 的位置）。当 3 放入到数组 R 中后，小于等于 3 的元素就只剩下了 6 个了，所以相应的 C[3]要减 1，变成 6。

from typing import List
import itertools


def counting_sort(a: List[int]):
    if len(a) <= 1: return

    # a中有counts[i]个数不大于i
    counts = [0] * (max(a) + 1)
    for num in a:
        counts[num] += 1
    # 对数组顺序求和
    counts = list(itertools.accumulate(counts))

    # 临时数组，储存排序之后的结果
    a_sorted = [0] * len(a)
    for num in reversed(a):
        index = counts[num] - 1
        a_sorted[index] = num
        counts[num] -= 1

    a[:] = a_sorted

计数排序只能用在数据范围不大的场景中，如果数据范围 k 比要排序的数据 n 大很多，就不适合用计数排序了。而且，计数排序只能给非负整数排序，如果要排序的数据是其他类型的，要将其在不改变相对大小的情况下，转化为非负整数。

3. 基数排序（Radix sort）

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

def radix_sort(res, d):
    for k in range(d):  # d轮排序
        # 每一轮生成10个列表
        s = [[] for i in range(10)]  # 因为每一位数字都是0~9，故建立10个桶
        for i in res:
            # 按第k位放入到桶中
            s[i // (10 ** k) % 10].append(i)
        # 按当前桶的顺序重排列表
        cur = [j for i in s for j in i]
        # 更新原数组
        res[:] = cur
    return res